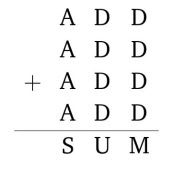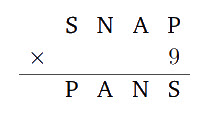Prepare for AMO 2019 – Grade 6 – Đề luyện thi toán tiếng anh AMO 2019 – Khối 6
Table Of Contents
Prepare for AMO 2019 – Grade 6
Week 1
Exercise 1. A fruiterer has a certain number of apples. If he arranges them in groups of 2, 3, 4, 5, 6, 7, 8 or 9, he will always have one left over for each gruop. What is the least number of apples he can possibly have?
Exercise 2. In the puzzle (cryptarithm) below, each letter stands for the different digit.
Find the sum A + B + C + D.
Exercise 3. Each of the integers 334 and 419 has digits whose product is 36. How many 3-digit positive integers have digits whose product is 36?
Exercise 4. For how many whole numbers from 5001 to 5499 does the product of the middle two digits exceed 6?
Exercise 5. How many of the first 2019 numbers in the sequence 101, 1001. 10001. 100001…. are divisible by 101?
Exercise 6. Mr Lim has two children, Darius and Elaine. Elaine is 18 years old. Given that the LCM of Darius’ age and Elaine’s age is 180, find Darius’ age given that he is less than 30 years.
Exercise 7. For how many whole numbers from 5001 to 5499 does the product of the middle two digits exceed 6?
Exercise 8. Find the smallest value of an integer P such that the LCM of P and 24 is 72.
Exercise 9. There is a sequence of consecutive positive integers on the board. Exactly 52% of them are even numbers. How many odd numbers are there on the board?
Week 2
Exercise 1. In the triangle shown, the first diagonal line, 1.2.3, 4,…, begins at 1 and each number after the first is one larger than the previous number. The second diagonal line, 2. 4.6, 8, … begins at 2 and each number after the first is two larger than the previous number. The nth diagonal line begins at n and each number after the first is n larger than the previous number. In which horizontal row does the number 2025 first appear?
Exercise 2. In the cryptarithm shown, each letter represents a different digit. How many possible values of 3-digit number “SUM” are there? A cannot equal 0.
Exercise 3. Phineas forms an ordered list consisting of seven consecutive whole numbers. The sum of the first, third, and sixth of these numbers is 175. Find the sum of the remaining four whole numbers.
Exercise 4. In the puzzle (cryptarithm) below, each letter stands for the different digit.
Find the sum A + B + C + D.
Exercise 5. Dr. Know – Everything wrote his name consecutively in a row like this:
KNOWEVERYTHINGKNOWEVERYTHINGKNOWEVERYTHING…
What is the 2019th letter?
Exercise 6. A book has 500 pages numbered 1, 2.3 and so on. How many times does the digit 1 appear in the page numbers?
Exercise 7. In the addition shown, P and Q each represent single digits, and the sum is 1PP7.
What is P + Q?
Exercise 8. The ages of two grandchildren are the digits of the age of the grandmother. The sum of their ages is 72. How old is the grandmother?
Exercise 9. Find the missing number.
Week 3
Exercise 1. Laura decorated each of her 24 cookies. She decorated 15 cookies with green colour and 13 cookies with blue colour. How many cookies were decorated with both green and blue colour?
Exercise 2. Mr. Cho received a container of fresh eggs. He sold 1/3 of the eggs in the morning and sold 320 eggs in the afternoon. At the end of the day, he found that 1/4 of the eggs were not sold. How many eggs did he receive in the beginning?
Exercise 3. Cindy saved $15 in the first month, $30 in the second month, $45 in the third month, and so forth. The amount of money she saved in the last month was $120. How much money did Cindy save in total?
Exercise 4. Round down
to the nearest whole number.
Exercise 5. Harry and Terry are each told to calculate 8 – (2 + 5). Harry gets the correct answer. Terry ignores the parentheses and calculates 8 – 2 + 5. If Harry’s answer is H and Terry’s answer is T, what is the value of T – H?
Exercise 6. The 7-digit numbers 74452B1 and 326AB4C are multiples of 3. Which one of the following is the value of C?
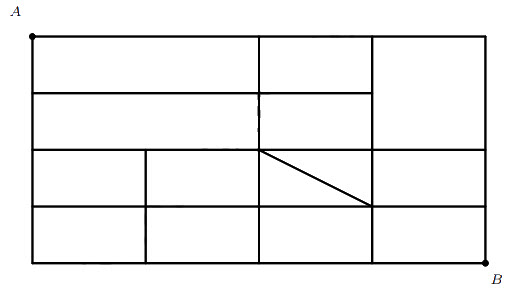
Exercise 7. What is the number of shortest paths from A to B?
Exercise 8. Sam has two identical wooden pyramids, each with a square base. He glues the two bases together to make a new bigger wooden shape. How many vertices are there in the new bigger shape?
Exercise 9. When you multiply Sophie’s age and Sony’s age, you get 36. If you add their ages together, you get 15. Sophie is older than Sony. How old is Sony?
Week 4
Exercise 1. Except for the first term, each term in the following sequence is found by multiplying the same number to the previous term.
3, a, b, c, 48, …
Find the value of c.
Exercise 2. Find the value of n if n is a whole number and 1/n is more than 8/143 but less than 6/97.
Exercise 3. A big cube is made up of 125 small cubes. All the faces of the big cube are then painted.
How many of the small cubes have exactly two painted faces?
Exercise 4. If the four-digit number 4N79 is divisible by 21, find N.
Exercise 5. If 5 men take 3 days to build 2 walls, how many days will it take 8 men to build 16 walls? Assume that all the men work at the same rate.
Exercise 6. The 7-digit numbers 74A452B1 and 326AB4C are multiples of 3. Which one of the following is the value of C?
Exercise 7. In the following alphametic, all the different letters stand for different digits. Find the sum of 4 digit P, A, N, S.
Exercise 8. Alice bought some strawberries and gave half of them to Bryan. Bryan bought some peaches and gave half of them to Alice. After Alice had eaten 3 peaches, the ratio of the number of peaches to the number of strawberries she had was 1 : 4 . After Bryan had eaten 8 strawberries, the ratio of the number of peaches to the number of strawberries he had was 1: 3. How many peaches did Bryan buy?
Exercise 9. The diagram shows parts of a city where the lines are roads. Trevor walks from point X to point Y along the roads without ’backtracking’ (i.e. he can only walk upwards or to the right in the diagram below). How many ways can he walk from X to Y?
Hits: 34