Grade 9 Olympiad – Tuyển chọn câu hỏi Olympiad lớp 9
Table Of Contents
Grade 9 Olympiad
Week 1
Choose correct answer(s) from the given choices
(1) Given the following equations:
5(a+b) = 3125, and 3125(a-b) = 5, what is the value of b?
a. \frac{11}{5}
b. \frac{11}{7}
a. \frac{9}{5}
a. \frac{12}{5}
(2) A ΔABC is inscribed in a circle of radius 4cm. if ∠A = 600, AC – AB = 4cm and the area of ΔABC is x cm2, find the value of x2.
a. 213 b. 64 c. 24 d. 192
(3) If N = 11112, , find the 6th, digit in the expansion of N from the right.
a. 4 b. 3 c. 2 d. 0
(4) You are given a set of tiles which are numbered from 1 to 121. You do the following operations repeatedly: you remove all those tiles that are numbered with a perfect square, and renumber the remaining tiles consecutively starting with 1. How many times must you perform the operation before you are left with 1 tile?
a. 18 b. 20
c. 21 d. 22
(5) If x39 + 69 is divided by (x + 1), find the remainder.
a. 0 b. 69
c. 71 d. 68
Fill in the blanks
(6) A cube is painted with blue colour on its all six faces. If this cube is cut into equal small cubes, ……….. small cubes will have at least one face coloured.
(7) In a circle with center O, if OA = 17 cm, CD = 2 cm and OD is perpendicular to AB, then AB is ………. cm.
Answer the questions
(8) A ship docks at the port on 5 different days at 7:15 AM, 9:45 AM, 9:30 AM, 9:15 AM and
10:00 AM.
What is the average time it docks?
\left( {6666 + \frac{1}{{3333}}} \right)\left( {6666 + \frac{1}{{3333}}} \right) - \left( {6666 - \frac{1}{{3333}}} \right)\left( {6666 - \frac{1}{{3333}}} \right) = ?
(10) If x + y – 2t = 0 then find the value of \frac{x}{{x - t}} + \frac{t}{{y - t}}
Week 2
Choose correct answer(s) from the given choices
(1) A cube is painted with red colour on its all six faces. If this cube is cut into equal 216 small cubes, how many small cubes will have no face coloured?
a. 1 b. 36
c. 64 d. 5
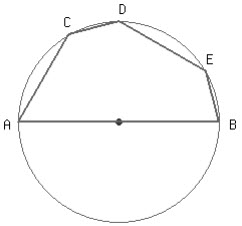
(2) If AB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD + ∠BED
a. 235° b. 360°
c. 270° d. 180°
(3) The perimeter of a triangle is 44 cm. One side of a triangle is 2 cm longer than the smallest side and the third side is 2 cm less than 2 times the smallest side. Find the area of the triangle.
a. 70 cm2 b. 105.6 cm2
c. 66 cm2 d. 22 cm2
(4) If Caleb drives at three fourth of his usual speed, he covers a certain distance in 3 hours more than the time he takes while driving at his usual speed. Find the time taken by him to cover this distance with his usual speed.
a. 8 hours b. 10 hours
c. 9 hours d. 11 hours
(5) How many 4 digit numbers are there that have at least one digit that is a 7 or a 8?
a. 5416 b. 8105
c. 3389 d. 5924
(6) Factorize (7x + 5)2 – 140x.
a. (x – 1) (49x – 25)
b. (x + 1) (49x – 25)
c. (7x – 5) (7x – 5)
d. (7x + 5) (7x – 5)
Fill in the blanks
(7) If AB is a diameter of the circle and C, D, E are any three points on the semi-circle.
∠ACD + ∠BED is °.
(8) The Ferris Wheel at the school fair has radius of 16 metres. It revolves at the rate of one revolution per 1 minute. A rider will travel from the bottom of the wheel to a point 8 vertical metres above the bottom in ………… seconds.
Answer the questions
(9) You are given a set of tiles which are numbered from 1 to 100. You do the following operations repeatedly: you remove all those tiles that are numbered with a perfect square, and renumber the remaining tiles consecutively starting with 1. How many times must you perform the operation before you are left with 1 tile?
(10) Find the area of the unshaded region in the figure below:
Week 3
Choose correct answer(s) from the given choices
(1) If N = 11112, find the sum of digits in the expansion of N.
a. 9 b. 8
c. 16 d. 12
Fill in the blanks
(2) If 1.111…… is written as p/q, such that p and q are positive integers without any common factor, the value of p+q is …………….
(3) Joseph and Brooke sit on the 8-member board of directors for company X. If the board is to be split up into two 4-person subcommittees, then the percentage that Brooke and Joseph are included in the same sub-committee is %.(Answer with two decimal places.)
Answer the questions
(4) The letters of the word STATISTICAL are rearranged in a random order. What is the probability that the letters C and L have exactly 3 letters between them?
(5) If a cone and a hemisphere stand on equal base and have the same height, find the ratio of their volumes.
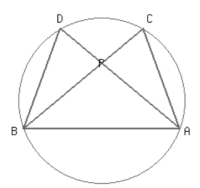
(6) If ∠ADB = 70° and ∠APB = 100°, find angle ∠DAC.
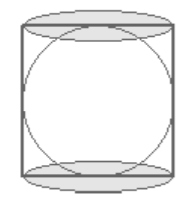
(7) A sphere is just enclosed inside a right circular cylinder. If the curved surface area of the cylinder is 60 cm2, find the surface area of the sphere.
(9) Find the volume of the biggest cone that can fit inside a cube of side 2 cm.
(10) Maria reaches her office 15 minutes early by traveling at a speed of 30 km/h and reaches 20 minutes late by traveling at a speed of 20 km/h. By how much time will she be early or late if she travels at 25 km/h?
Hits: 0